|
|
|
Кентерберийские
головоломки |
|
|
1
2
3
4
|
|
|
|
|
Головоломка Монахини.
- Уверена, что среди вас нет ни одного, - сказала Монахиня при одной из следующих
оказий, - кто не знал бы, что многие монахи часто проводят время в играх, которые не
очень-то приличествуют их сану. Карты или шахматы они искусно прячут от глаз аббата на
полках своих келий в толстых фолиантах, в которых внутри вырезают для этого
углубления. Стоит ли после этого сурово порицать монахинь за то, что они поступают так
же? Я покажу маленькую игру-головоломку, в которую мы иногда играем между собой,
когда наша добрая аббатиса отлучается из монастыря.

С этими словами Монахиня достала восемнадцать карт, показанных на рисунке. Она
объяснила, что головоломка состоит в том, чтобы сложить из этих карт колоду, причем,
если затем выложить верхнюю карту на стол, следующую - в низ колоды, следующую -
опять на стол, следующую - снова в низ колоды, пока все карты не окажутся на столе, то в
результате должны получиться слова CANTERBURY PILGRIMS (Кентерберийские
паломники (англ.). - Примеч. пер.). Разумеется, каждую следующую карту нужно
выкладывать на стол непосредственно справа от предыдущей. Это достаточно легко
выполнить, если двигаться в обратную сторону, однако читатель должен попытаться
получить ответ, не проделывая такой обратной операции и не пользуясь настоящими
картами.
|
|
|
|
|
|
|
Головоломка Купца
Купец, который был среди паломников, отличался тем, что "курс
экю высчитывать умел и знатно на размене наживался" и "... так искусно вел свои расчеты,
Что пользовался ото всех почетом". Однажды утром, когда вся компания двигалась по
дороге, Рыцарь и Сквайр, ехавшие рядом с Купцом, напомнили ему, что он все еще не
порадовал компанию своей головоломкой.

- В самом деле? - оживился купец. - Тогда вот вам числовая головоломка, которую я
предложу всей честной компании, когда мы остановимся отдохнуть. Сегодня утром нас
движется по дороге тридцать человек. Мы можем двигаться один за другим, что
называется, гуськом, или пара за парой, или тройка за тройкой, или пятерка за пятеркой,
или шестерка за шестеркой, или десятка за десяткой, или, наконец, все тридцать в ряд.
Ехать каким-либо иным способом, так, чтобы в каждом ряду всадников было поровну, мы
не можем. А вот некая компания паломников способна ехать шестьюдесятью четырьмя
способами. Скажите мне, сколько в этой компании должно быть паломников.
Купец, очевидно, имел в виду наименьшее число всадников, которые могут ехать
шестьюдесятью четырьмя способами.
|
|
|
|
|
|
|
Головоломка Юриста
"Был с ними важный, чопорный Юрист. Он, как искусный,
тонкий казуист. На паперти был очень уважаем И часто на объезды назначаем". Вообще он
был человеком весьма занятым, но, как и многие в наши дни, "работник ревностный, пред
светом целым, Не столько был им, сколько слыть умел им". Однажды вечером, говоря о
темницах и узниках, он заметил по ходу дела:
- То, о чем я говорил, напомнило мне о головоломке, которую я придумал сегодня утром,
чтобы предложить вашему вниманию.
С этими словами Юрист вынул кусок пергамента, на котором был изображен странный
план, приведенный на рисунке.
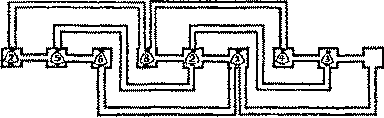
- Вот здесь, - сказал он, - изображены девять темниц. В каждой из них, кроме одной,
находится по узнику. Эти узники пронумерованы в порядке 7, 5, 6, 8, 2, 1, 4, 3. Я хотел бы
знать, как их можно расположить в порядке 1, 2, 3, 4, 5, 6, 7, 8 за наименьшее число
перемещений. Одного узника за один раз можно перевести по переходу в пустующую
темницу, но под страхом смерти запрещается двум узникам находиться одновременно в
одной темнице. Как же решить задачу?
Если читатель набросает примерный план на листе бумаги и "воспользуется
пронумерованными фишками, то он сможет с интересом провести время, стараясь
переместить узников за наименьшее число ходов. Поскольку на каждом ходе свободной
оказывается только одна темница, последовательность перемещений можно записать
весьма простым способом: 3-2-1-6 и т. д.
|
|
|
|
|
|
|
Головоломка Ткача
Когда Ткач развернул квадратный кусок ткани с искусно
вышитыми львами и замками, паломники стали обсуждать между собой, что мог бы
означать этот орнамент. Однако Рыцарь, будучи искушен в геральдике, пояснил, что
скорее всего он происходит от львов и замков, украшавших доспехи Фердинанда III, короля
Кастилии и Леона, дочь которого была первой женой английского короля Эдуарда I. В этом
он был, несомненно, прав. Головоломка же, предложенная Ткачом, была такова:
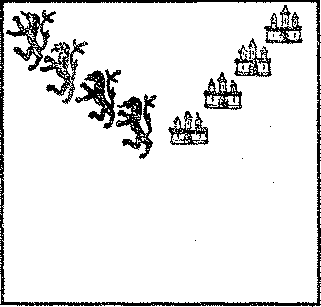
- Давайте посмотрим, ради всего святого, - сказал он, - найдется ли кто-нибудь в этой
компании, кто может показать, как следует разрезать кусок ткани на четыре части
одинакового размера и формы, чтобы при этом на каждой части оказалось ровно по
одному льву и замку.
Записи не говорят, удалось ли кому-нибудь решить эту головоломку, хотя ее вполне можно
решить удовлетворительным образом. Никакой разрез не должен пересекать льва или
замок.
|
|
|
|
|
|
|
Головоломка Повара
В компании паломников был и Повар. Его искусство,
несомненно, пользовалось огромным признанием, ибо "Умел варить, тушить он, жарить,
печь; Умел огонь как следует разжечь; Похлебку он на славу заправлял; Эль лондонский
тотчас же узнавал". Однажды вечером, когда паломники в деревенской харчевне
собирались приступить к трапезе, Повар встал у стола, возглавляемого Франклином
(Франклин - зажиточный земельный собственник из старых деревенских англосаксонских
родов. - Примеч. пер.), и сказал:

- Послушайте меня, господа мои, я задам вам одну головоломку. Клянусь святым
Моденом, она из тех задач, на которые я сам не могу ответить. Одиннадцать паломников
сидят за этим столом, на котором стоят пирог и блюдо с паштетом из оленьей печенки. И
паштет, и пирог можно разделить на четыре части, но не больше. Теперь заметьте, пятеро
из нас любят пирог, но не прикоснутся к паштету, тогда как четверо обожают паштет, но
воротят нос от пирога. Двое же оставшихся желают отведать оба блюда. Во имя всего
святого, найдется ли кто-нибудь среди вас, кто смог бы мне сказать, сколькими способами
этот достойный Франклин может выбрать тех, кого он захочет угостить?
Я должен сразу же предупредить читателя: если он будет невнимателен, то, заглянув в
ответ, обнаружит, что ошибся на 40, как это и произошло со всей компанией. Только
Оксфордский студент дал правильный ответ, да и то случайно - он попросту описался.
Удивительно, но пока компания сидела, погрузившись в задумчивость, Повар произвел
какие-то манипуляции. Что же мог сделать этот хитрец посреди столь глубоких
размышлений, как не стащить украдкой оба блюда! Когда голод заставил путников опять
обратиться к трапезе, они обнаружили, что стол-то пуст. Тут все шумно потребовали у
Повара объяснений.
- Господа мои, - объяснил он, - поняв, как трудна для вас эта головоломка, я отнес
блюда в соседнюю комнату, где наши спутники с удовольствием их съели, пока они не
остыли. Зато в здешней кладовой я обнаружил прекрасные хлеб и сыр.
|
|
|
|
|
|
|
Головоломка Пристава церковного суда
Пристав, путешествовавший с компанией
паломников, был должностным лицом, в обязанности которого входило вызывать виновных
в церковные суды. По признанию Чосера, "Он угреват был, глазки - словно щелки. И
валик жиру на багровой холке. Прожженный он игрок был и гуляка. Лихой добытчик,
дерзкий забияка. За кварту эля он бы разрешил Блудить пройдохе, хоть бы тот грешил
Напропалую, с простака ж он шкуру Сдирал, чтоб рот не разевал тот сдуру".
Однажды десять паломников остановились у деревенской таверны и потребовали себе
ночлега; но хозяин мог принять только пятерых из них. Пристав предложил бросить
жребий, а поскольку за время службы он поднаторел в таких делах, то поставил всех в круг
и предложил счет "на вылет". Будучи все же рыцарем по натуре, он замыслил устроить
дело таким образом, чтобы вылетели все, кроме дам. И вот он шепнул Батской ткачихе
номер и велел ей считать по кругу по часовой стрелке; тот, на кого выпадет номер,
выбывал из круга. Затем счет следовало начать заново со следующего по порядку
человека. Однако леди кое-что недопоняла, а потому выбрала число 11 и начала счет с
себя. В результате вместо мужчин выбыли по очереди все женщины, ибо каждой
одиннадцатой в исходном круге была женщина.

- По правде говоря, это не моя ошибка, - сказал на следующий день Пристав всей
компании, - а вот, кстати, и головоломка. Может ли кто-нибудь сказать, каким числом
должна была воспользоваться Батская ткачиха и с кого из паломников следовало ей
начать счет, дабы выбыли из круга пятеро мужчин?
Разумеется, нужно найти наименьшее из подходящих чисел.
|
|
|
|
|
|
|
Головоломка Монаха
Монах, ехавший со всей компанией, был большим любителем
спорта. "Наездник страстный, он любил охоту и богомолье - только не работу". Однажды,
обратясь к паломникам, он сказал:
- Есть одна вещь, которая заставляет меня порой сильно задумываться, хотя, конечно,
она не столь и важна. Все же она может служить для проверки остроты ума.

Я имею девять будок для собак, они расположены в форме квадрата, хотя среднюю конуру
я не использую. Так вот, головоломка состоит в том, чтобы выяснить, сколькими
различными способами могу я поместить своих собак во всех наружных будках так, чтобы
число собак на каждой стороне квадрата равнялось десяти.
Небольшие диаграммы, приведенные на рисунке, показывают четыре таких способа, и хотя
четвертый способ является лишь перевернутым третьим, он считается отличным от
третьего. Любую будку можно оставить пустой. Эта головоломка, очевидно, представляет
собой лишь разновидность известной головоломки об аббатисе и ее монахинях.
|
|
|
|
|
|
|
Головоломка Шкипера
Об этом персонаже нам известно, что "Корабль он вел без
карт и без промера От Готланда до мыса Финистера, Все камни знал Бретонских берегов;
Все входы бухт испанских и портов; Немало бурь в пути его встречало И выцветшую
бороду трепало; От Гулля и до самой Картахены Все знали капитана "Маделены".

- Вот это карта, - сказал Шкипер, - пяти островов, с жителями которых я веду торговлю.
Каждый год мой славный корабль ходит по всем десяти указанным здесь путям, но никогда
в один и тот же год я не хожу ни по одному пути дважды. Есть ли среди вас кто-нибудь, кто
мог бы мне сказать, сколькими различными способами "Маделена" сможет совершить эти
десять ежегодных плаваний, отправляясь всегда от одного и того же острова?
|
|
|
|
|
|
|
Головоломка Аббатисы
Аббатиса, которая путешествовала под именем Эглантина,
по замечанию Чосера, "И по-французски говорила плавно, Как учат в Стратфорде, а не
забавным Парижским торопливым говорком". Однако наша головоломка имеет отношение
не столько к ее характеру и образованию, сколько к ее одежде. "Был ладно скроен плащ ее
короткий, А на руке коралловые четки Расцвечивал зеленый малахит. На фермуаре
золотой был щит С короной над большою буквой А". Именно эта брошь нас и интересует,
поскольку, когда очередь задать головоломку дошла до Аббатисы, она показала это
украшение всей компании и сказала:
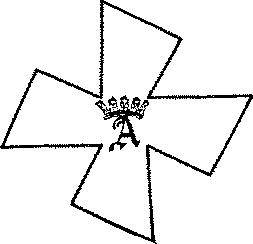
- Один образованный человек из Нормандии подарил мне некогда эту прелестную
вещицу, сопроводив это какими-то странными мистическими словами о том, что будто бы
она родственна квадрату, или что-то в этом роде, чего я совершенно не могла понять. Но
добрый аббат из Чертей сказал мне, что этот крест можно искусно разрезать на четыре
части, из которых затем удастся сложить правильный квадрат, хотя, клянусь верой, я не
знаю, как это сделать.
Записи гласят, что паломники не смогли решить эту головоломку, и Оксфордский студент
заключил, что Аббатиса все напутала. Леди это весьма раздосадовало, хотя благородный
Рыцарь подверг бедного студента насмешкам - ведь тот сам прежде не справился с
головоломкой, так что студент устыдился, а компания развеселилась.
|
|
|
|
|
|
|
Головоломка Доктора медицины
Этот Доктор, хотя и слыл образованным
человеком, ибо "С ним в ремесле врачебном ни единый Врач лондонский соперничать не
мог", так как "прекрасно знал болезней он истоки", не был чужд греховной страсти
стяжательства. "...Тратился он неохотно, Со дней чумы сберег мешочек плотный; И золото
- медикамент целебный - Хранил, должно быть, как припас лечебный". Задача, которую
Доктор предложил собравшимся паломникам, состояла в следующем. Он вынул два
сферических сосуда и сообщил, что один из них имеет в окружности один фут, а другой -
два фута.

- Я хотел бы, - сказал Доктор, - знать точные размеры двух других сосудов той же
формы, но иного размера, которые вместе могли бы вместить ровно столько же жидкости,
сколько и эти два сосуда.
Найти точные размеры, выражающиеся наименьшими возможными числами, - это один
из самых крепких орешков, за которые я брался. Разумеется, мы пренебрегаем толщиной
стеклянных стенок сосуда, а также горлышком и подставкой.
|
|
|
|
|
|
|