|
Великий диспут между Кармелитом и Приставом церковного суда
Чосер сообщает
о том прискорбном факте, что гармония паломничества время от времени нарушалась
ссорами между Кармелитом и Приставом церковного суда. Однажды последний пригрозил
даже: "Свою побереги, приятель, кожу. И ты, монах, мне можешь плюнуть в рожу, Когда о
братьях истины позорной Всем не раскрою я до Сиденборна", но здесь вмешался до-
стойный Трактирщик и временно восстановил мир. К несчастью, ссора вспыхнула снова во
время одного весьма любопытного диспута. Дело было так.

В одном месте путь паломников должен был пролечь вдоль двух сторон квадратного поля,
и кое-кто из паломников настаивал, чтобы, не обращая внимания на заграждения,
двигаться из одного угла поля в другой, как они и делают это на рисунке. И тут Кармелит
поразил всю компанию, заявив, что нет нужды нарушать заграждения, ибо и при том, и при
другом способе придется преодолеть в точности одинаковые расстояния.
- Клянусь небом, - воскликнул Пристав, - ты сущий болван!
- Ничего подобного, - ответил Кармелит, - если только все выслушают меня терпеливо,
то я докажу, что это ты болван, ибо твой мозг слишком скуден для того, чтобы показать,
что диагональ квадрата меньше двух его сторон.
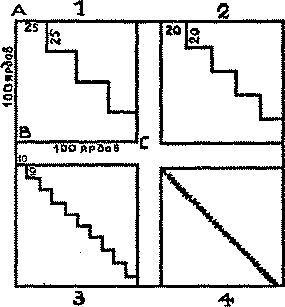
Если читатель обратится к приведенному здесь рисунку, то ему легче будет следить за
аргументами Кармелита. Предположим, что сторона поля равна 100 ярдам; тогда
расстояние вдоль двух сторон от А до В и от В до С равно 200 ярдам. Кармелит взялся
доказать, что расстояние по диагонали от А до С также равно 200 ярдам. Если мы будем
двигаться вдоль пути, показанного на рис. 1, то, очевидно, пройдем то же расстояние, ибо
длина каждого из восьми прямых участков равна в точности 25 ярдам. Аналогично зигзаг
на рис. 2 состоит из 10 прямых участков, по 20 ярдов в каждом; значит, весь путь равен 200
ярдам. Не важно, сколько прямолинейных участков будет в нашем зигзаге; результат,
совершенно ясно, будет тем же самым. Так, на рис. 3 "ступеньки" очень малы, и все же
расстояние равно 200 ярдам. То же происходит на рис. 4 и будет происходить даже в том
случае, когда "ступеньки" мы сможем различить лишь под микроскопом. Продолжая этот
процесс дальше, говорил Кармелит, мы будем выпрямлять наш зигзагообразный путь до
тех пор, пока он не превратится в совершенно прямую линию; а отсюда следует, что длина
диагонали квадрата равна сумме длин двух его сторон.
Но это заведомо ложное утверждение; его абсурдность мы можем проверить с помощью
непосредственного измерения, если у нас остаются какие-то сомнения. И все же Пристав
ни за что не мог опровергнуть Кармелита, отчего пришёл в такую ярость, что, не вмешайся
другие паломники, дело кончилось бы дракой. Быть может, читатель сразу обнаружит
слабое место в рассуждениях Кармелита?
|
|
В этой небольшой задаче мы пытались показать, как с помощью всяких софизмов на
первый взгляд удается доказать, что диагональ квадрата имеет ту же длину, что и две его
стороны. Головоломка состояла в том, чтобы найти ошибку в рассуждениях, ибо такая
ошибка, безусловно, есть, если мы считаем, что прямая реализует кратчайшее расстояние
между двумя точками. Но где же вкралась ошибка?
Ясно, что, коль скоро наш зигзаг составлен из "ступенек", параллельных сторонам
квадрата, его длина равна сумме длин двух сторон квадрата. Не важно даже, потребуется
ли вам, чтобы разглядеть эти ступеньки, мощный микроскоп. Но ошибка состоит в
допущении, что такой зигзагообразный путь может стать прямой линией. С помощью этого
метода даже при неограниченном (по крайней мере теоретически) увеличении числа таких
ступенек вы никогда не получите прямой линии. При переходе от зигзага с миллиардом
ступенек к прямой практически вы совершите такой же "скачок", как и в самом начале,
перейдя от двух сторон квадрата к его диагонали. Сказать, что, увеличивая число ступенек,
мы в конце концов получим прямую, так же абсурдно, как и утверждать, что, бросая
камешки в корзину, мы в конце концов получим золотые монеты. В этом-то и состояла вся
закавыка.
|