|
Головоломка Доктора медицины
Этот Доктор, хотя и слыл образованным
человеком, ибо "С ним в ремесле врачебном ни единый Врач лондонский соперничать не
мог", так как "прекрасно знал болезней он истоки", не был чужд греховной страсти
стяжательства. "...Тратился он неохотно, Со дней чумы сберег мешочек плотный; И золото
- медикамент целебный - Хранил, должно быть, как припас лечебный". Задача, которую
Доктор предложил собравшимся паломникам, состояла в следующем. Он вынул два
сферических сосуда и сообщил, что один из них имеет в окружности один фут, а другой -
два фута.

- Я хотел бы, - сказал Доктор, - знать точные размеры двух других сосудов той же
формы, но иного размера, которые вместе могли бы вместить ровно столько же жидкости,
сколько и эти два сосуда.
Найти точные размеры, выражающиеся наименьшими возможными числами, - это один
из самых крепких орешков, за которые я брался. Разумеется, мы пренебрегаем толщиной
стеклянных стенок сосуда, а также горлышком и подставкой.
|
|
Здесь мы действительно сталкиваемся с запутанной задачей. Наши учебники
сообщают, что все сферы подобны и что соответствующие объемы относятся, как кубы
линейных размеров. Следовательно, поскольку окружности (Здесь имеются в виду
окружности большого круга. - Примеч. Пер.) двух сосудов равны соответственно одному и
двум футам, а кубы единицы и двух в сумме дают 9, то нам остается только найти два
других числа, сумма кубов которых равнялась бы 9. Разумеется, эти числа должны быть
дробными. Кстати, этот маленький вопрос привлекал внимание образованнейших людей
своего времени на протяжении двух с половиной столетий. Хотя Ферма в XVII в. показал,
как можно найти ответ из двух дробей со знаменателем, содержащим не менее чем 21
цифру, этим исчерпываются не только все опубликованные ответы, полученные с
помощью его метода, который я нашел неточным, но и никогда не публиковавшийся много
меньший результат, приведенный ниже. Кубы чисел
(415 280 564 497)/(348 671 682 660) и (676 702 467 503)/(348 671 682 660)
в сумме дают ровно 9, и, следовательно, такими долями фута должны выражаться длины
окружностей двух сосудов, про которые Доктор сказал, что они должны вместе содержать
такое же количество жидкости, как и показанные два сосуда. Один выдающийся клерк
страховой компании и еще один корреспондент взяли на себя труд возвести в куб эти
числа, и они оба нашли мой ответ совершенно правильным.
Если бы исходные сосуды имели в окружности соответственно 1 и 3 фута, то ответом
служили бы числа
(63 284 705)/(21 446 828) и (28 340 511)/(21 446 828)
сумма кубов которых равна 28. (См. также головоломку 61.)
Зная какое-то выражение числа в виде суммы или разности двух кубов, мы можем по
формуле получить отсюда бесконечно много других представлений этого числа с помощью
попеременно положительных и отрицательных чисел. Так, Ферма, отправляясь от извест-
ного равенства 13 + 23 = 9 (которое мы назовем основным), сначала получил решение из
больших отрицательных чисел, а затем решение из еще больших положительных чисел.
Но существует бесконечно много основных соотношений, и я с помощью ряда проб нашел
исходное решение из отрицательных чисел (меньших, чем те, что на первом шаге получил
Ферма), из которого я уже и вывел решение, указанное выше. Это простое объяснение.
О любом числе до 100, за исключением 66, мы можем сказать, представимо ли оно в виде
суммы двух кубов или нет. Студентам следует обратиться к курсу теории чисел.
Несколько лет назад я опубликовал решение для случая
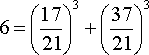 , ,
для которого Лежандр привел обстоятельное "доказательство" невозможности такого
представления, но я обнаружил, что Люка предвосхитил появление моего решения.
|