|
Головоломка Монаха
Монах, ехавший со всей компанией, был большим любителем
спорта. "Наездник страстный, он любил охоту и богомолье - только не работу". Однажды,
обратясь к паломникам, он сказал:
- Есть одна вещь, которая заставляет меня порой сильно задумываться, хотя, конечно,
она не столь и важна. Все же она может служить для проверки остроты ума.

Я имею девять будок для собак, они расположены в форме квадрата, хотя среднюю конуру
я не использую. Так вот, головоломка состоит в том, чтобы выяснить, сколькими
различными способами могу я поместить своих собак во всех наружных будках так, чтобы
число собак на каждой стороне квадрата равнялось десяти.
Небольшие диаграммы, приведенные на рисунке, показывают четыре таких способа, и хотя
четвертый способ является лишь перевернутым третьим, он считается отличным от
третьего. Любую будку можно оставить пустой. Эта головоломка, очевидно, представляет
собой лишь разновидность известной головоломки об аббатисе и ее монахинях.
|
|
Монах мог поместить собак в конуры 2926 различными способами так, чтобы на каждой
стороне было по 10 собак. Число собак может изменяться от 20 до 40; в этих пределах
всегда можно расположить собак нужным способом.
Решение этой головоломки в общем виде непросто. В случае n собак на каждой стороне
квадрата число различных способов равно
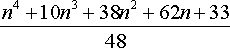 , ,
при n нечетном и
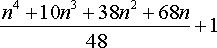 , ,
при n четном, если считать только те размещения, которые существенно различны. Но
если мы будем считать все перевернутые и отраженные размещения различными, как и
поступал сам Монах, то n (четное или нечетное) собак можно разместить
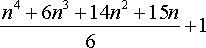 , ,
способами. Дабы возможно было поместить по n собак на каждой стороне, их число
должно быть не меньше 2n и не больше 4n, но внутри этих границ его можно взять любым.
Обобщение принципа, лежащего в основе этой головоломки, приведено в задаче 42.
|