|
|
|
Кентерберийские
головоломки |
|
|
|
|
Головоломка Юриста
"Был с ними важный, чопорный Юрист. Он, как искусный,
тонкий казуист. На паперти был очень уважаем И часто на объезды назначаем". Вообще он
был человеком весьма занятым, но, как и многие в наши дни, "работник ревностный, пред
светом целым, Не столько был им, сколько слыть умел им". Однажды вечером, говоря о
темницах и узниках, он заметил по ходу дела:
- То, о чем я говорил, напомнило мне о головоломке, которую я придумал сегодня утром,
чтобы предложить вашему вниманию.
С этими словами Юрист вынул кусок пергамента, на котором был изображен странный
план, приведенный на рисунке.
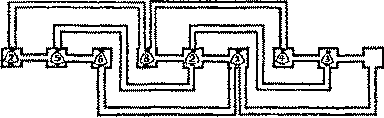
- Вот здесь, - сказал он, - изображены девять темниц. В каждой из них, кроме одной,
находится по узнику. Эти узники пронумерованы в порядке 7, 5, 6, 8, 2, 1, 4, 3. Я хотел бы
знать, как их можно расположить в порядке 1, 2, 3, 4, 5, 6, 7, 8 за наименьшее число
перемещений. Одного узника за один раз можно перевести по переходу в пустующую
темницу, но под страхом смерти запрещается двум узникам находиться одновременно в
одной темнице. Как же решить задачу?
Если читатель набросает примерный план на листе бумаги и "воспользуется
пронумерованными фишками, то он сможет с интересом провести время, стараясь
переместить узников за наименьшее число ходов. Поскольку на каждом ходе свободной
оказывается только одна темница, последовательность перемещений можно записать
весьма простым способом: 3-2-1-6 и т. д.
|
|
|
Наименьшее число шагов, за которое можно нужным образом расположить узников,
равно 26. Узники передвигаются в следующем порядке: 1, 2, 3, 1, 2, 6, 5, 3, 1, 2, 6, 5, 3, 1, 2,
4, 8, 7, 1, 2, 4, 8, 7, 4, 5, 6. Поскольку свободной всегда оказывается только одна темница,
эти обозначения не могут вызвать недоразумений.
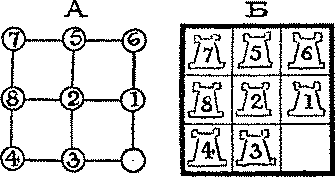
Эту диаграмму можно упростить с помощью так называемого метода "пуговок и веревочек".
В результате получатся диаграммы, изображенные на рисунке, которые намного упростят
решение. В случае А можно использовать фишки, в случае Б можно воспользоваться
шахматными ладьями и уголком шахматной доски. В обоих случаях мы приходим к
расположению
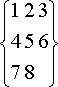
за наименьшее возможное число шагов. См. также решение
головоломки 94.
|
|
|
|